約数と倍数 a = kb(a,b,k ∈ Z,b = 0) を満たすkが存在する時bはaの約数、 aはbの倍数 aはbで割り切れるといいb∣aとかく 倍数 は簡単です。ある数字の倍数はある数字を2倍・3倍・4倍・・・とした時に得られる数字のことです。 2の倍数は $$2,4,6,8,10,12,14,16,18,,22,\cdots$$ となりますね。ここでも公約数と同じように2つ以上の数字を考え、共通の倍数を考えることにしましょう。 素因数分解とは?やり方やコツ、利用問題(約数など) 最大公約数・最小公倍数 小学校で習う最大公約数・最小公倍数は、高校数学でも重要な意味をもちます。 最大公約数とは?意味や簡単な求め方、計算問題 最小公倍数とは?求め方や計算問題、最大

最大公約数の求め方 素因数分解を使った解き方のコツとは 高校生向け受験応援メディア 受験のミカタ
約数と倍数 高校
約数と倍数 高校-約数と倍数 - カテゴリー 全 4 件の記事が見つかりました。 19年7月30日 最大公約数と最小公倍数の計算方法 最大公約数と最小公倍数の計算方法を解説します。 まず、基本的な計算方法として、素因数分解を用いた計算方法を復習したいと思います高校1年 (本時) (単元) 正の数・負の数 の指導内容) (学習指導要領 A 高校1年 ) 数と式 (単元) 文字を用いた式 の四則演算 (学習指導要領 の指導内容) 数と式 数と式 約数と倍数 (単元) 整数の性質 (学習指導要領 の指導内容) 数学A (2




高校生 約数と倍数のノート一覧 Clear
約数と倍数 その3|受験算数アーカイブス 当サイトは受験生のお子様を持つ方々,中学受験算数を教えている・教えたい方々,算数・数学が好きな方々,など幅広い『大人のための』中学受験算数解説サイトです. TOP > 数の性質 > 約数と倍数 その3 基本編(約数、公倍数公約数)の実践編です。 (1)約数の数が3個あり、約数を全て足すと463になる自然数を求めなさい。 (2)504の約数の中で、4の倍数である約数の総和を求めなさい。 (3)150の約数の逆数の和と221 約数と倍数 211 除法の原理 整数の和,差,および積は整数となるが商については,常に整数になるとは限らない. 以下の内容は,各々具体例を生徒に考えさせながら定着を図ることとする. Item_1 《約数と倍数》 2 つの整数a ,b( bz0 )に対して商 a b
約数と倍数・倍数の判定方法の説明のおわりに いかがでしたか? 倍数判定方法を忘れてしまった場合には、実際に割ってみて割り切れるかどうかを確認すれば問題ありません。 その数の倍数であるかどうかはその数を約数に持つかどうかですので 高校1年生 数A約数と倍数授業ノート 🍥約数と倍数 🍥倍数の判定法 🍥素因数分解 🍥等式を満たす整数x,yの組 参考教科書:新編数学A 数研出版 このノートが参考になったら、著者をフォローをしませんか? 気軽に新しいノートをチェック 正の整数の約数の総和を表す公式を2つ紹介します。 1つ目は入試でも頻出の必須公式です。 2つ目はコサインが出てくる観賞用の公式です。玄人向け。 なお,約数の個数に関しては約数の個数の公式と平方数の性質を参照して下さい。
約数と倍数 その1 今回は「約数・倍数」に注目して,典型的な問題の考え方を見てゆきたいと思います.公約数・公倍数の基本的な意味や求め方に不安があれば, こちら (すだれ算の基本) を参考にしてください. ではさっそく問題です. 問題1:1から50 整数の性質|約数と倍数について 今回から「整数の性質」の単元になります。 まず学習するのは、約数と倍数についてです。 小中学校で学習した内容の続きになるので、忘れていないか確認しながら取り組みましょう。 1 約数と倍数、倍数の判定法6講 合同式(1節 約数と倍数) 問題集3章 整数の性質です。わかりやすいポイントと例題つきの問題集です!定期テスト対策にお使いください。全て無料でダウンロードできます。塾や家庭教師、学校でご自由にお使いください!



最大公約数の意味と求め方 約数がいくつあるか簡単に調べる方法とは アタリマエ




高校生 約数と倍数のノート一覧 Clear
前回 https//googl/UwgSgk 次回 https//googl/9vCW59動画のプリント(19ch) http//www19chtv/サブチャンネル とある男が高校入試の難問 開成10 開成高校の数学の入試問題です。 10について,次の問いに答えなさい。 (1)素因数分解せよ。 (2)正の約数の総和を求めよ。 (3)10との最大公約数が1となる4桁の正の整数の個数を求めよ。 (4)最小公倍数が10となるMathAquarium例題整数の性質 1 整数の性質 1 倍数の性質 a,b は整数とする。a+b,a が3 の倍数ならば,b は3 の倍数であることを証明せよ。 要点 整数a と0 でない整数b に対して, a=bk となる整数k があるとき,a はb の 倍数 であるという。 0 はすべての整数の倍数である。




高校数学a 自然数の分類と素因数分解の一意性 受験の月



高校二年生数学aの整数の性質 約数と倍数 素因数分解のところで Yahoo 知恵袋
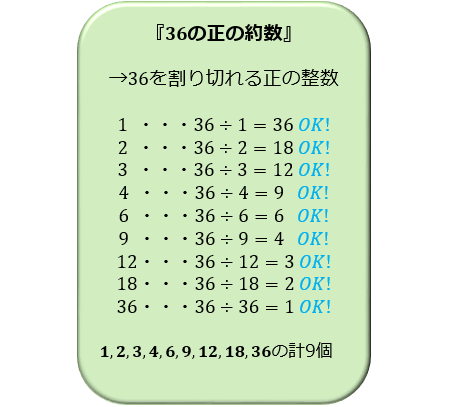
(1)48の約数は全部で 個あります。 (2)50以上の素数で2番目に小さい数は です。 (3)255、459、1122の最大公約数は です。 (4)36、60、84の最小公倍数は です。 (5)2けたの整数で、6の倍数で144の約数でもあるのは 個あります。 ある数が $60$ の約数であるかどうかを考えてみます。 例えば、 $2,3,4,5,6$ は $60$ の約数ですが、 $7,8,9$ は $60$ の約数ではありません。 $10,12,15$ は約数で、 $11,13,14$ は約数ではありません。なんだかきれいな法則はないように見えますね。 高校1年生 ①約数と倍数 約数と倍数 倍数の判定法 素因数分解 最大公約数と最小公倍数 割り算における商と余り 余りによる整数の分類 ②ユークリッドの互除法 ユークリッドの互除法 1次不定方程式 2次不定方程式 ③整数の性質の活用 有理数の小数表現 n進法




倍数と約数の教え方 4 約数の個数 ママのための受験算数の教え方プチ講座 中学受験ナビ




高校数学 数a 5 場合の数 正の約数編 Youtube
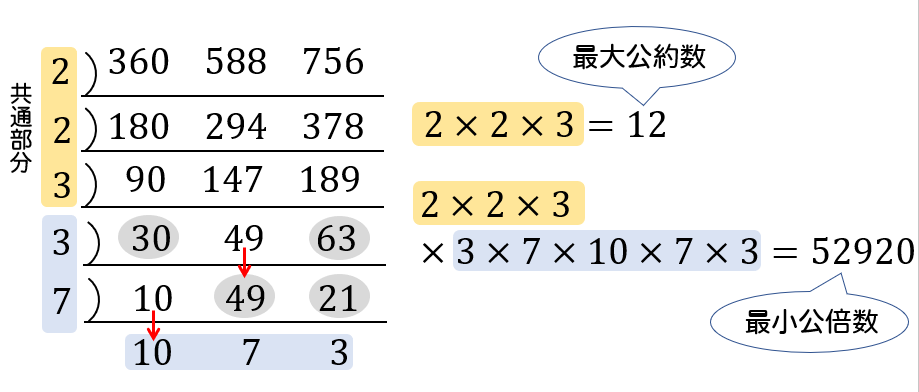
A,bが5の倍数ならば,2a-3bは5の倍数であることを証明せよ。 証明 a,bが5の倍数であるから,整数k,lを用いて, a=5k,b=5l と表すことができる。 よって 2a-3b=2・5k-3・5l=10k-15l=5(2k-3l) 2k-3lは整数であるから,2a-3bは5の倍数である。 2 最小公倍数は、最大公約数とそれぞれのオリジナル因数を取り出して掛け合わせた値になります。 なので、素因数分解をした式を書き並べ、 それぞれの因数の個数が大きいものを取り出していけばOKです。 答え (1)最大公約数 , 最小公倍数 次に(2)3整数の性質とは第5 学年で偶数,奇数,約数, 倍数について学ぶことである。約数と倍数は小学 校第6 学年から移行した内容である。そのため, 今回の実践で対象となる児童はすべて約数,倍数 についてすでに学習しており,既習事項を深めて いくことに




約数の個数の求め方 素因数分解すれば一発で求まる 高校生向け受験応援メディア 受験のミカタ




倍数と約数の教え方 4 約数の個数 ママのための受験算数の教え方プチ講座 中学受験ナビ
約数 約数ある整数を割り切れることができる整数。 18の約数1、2、3、6、9、18 素数約数が1とその数しかない整数 2、3、5、7、11、13、17、1講 約数と倍数(1節 約数と倍数) 問題集3章 整数の性質です。わかりやすいポイントと例題つきの問題集です!定期テスト対策にお使いください。全て無料でダウンロードできます。塾や家庭教師、学校でご自由にお使いください! 約数も倍数も、負の整数の場合がありえる、ということに注意しましょう。 例えば、 6 6 の約数は、 1,2,3,6 1, 2, 3, 6 だけでなく、 −1,−2,−3,−6 − 1, − 2, − 3, − 6 を合わせた8個、となり



高校一年生です フォーカスゴールド数1 Aのp438のstepu Yahoo 知恵袋



Studydoctor約数 倍数とは その求め方 Studydoctor
約数 倍数って必ず整数ですか? なんでですか? 教科書に書いてありますか?「倍数や約数は必ず整数である」と言う記述を見た記憶はありませんが、倍数や約数と言う概念の趣旨から言えば「整数に限定される」と言う事は読み取れるはず 約数・倍数とあまり① 今月は苦手な子の多い「約数・倍数とあまり」を、 第1回 問題文を式にする 第2回 5パターンの区別をつける/ 公式化する 第3回 公式を利用する/ 混合タイプをマスターする の、全3回にわけて一緒に勉強していきましょう。 動画 約数と倍数の問題です。 まずは約数と倍数の定義を確認する問題から。 素因数分解の一意性もテーマに含まれています。 1. B (東京工業大) 自然数 が を満たし, が を割り切るような自然数 は に限るとする. (1) は3と5で割り切れることを示せ. (2) の




O0wykgjnwgqwam




競プロ 素因数分解と約数と倍数 なかけんの数学ノート




高2 因数定理と整式の倍数 約数 高校生 数学のノート Clear




高校 数学a 整数9 約数の求め方 10分 Youtube




高校数学a 整数の性質 教科書 問題 解答 公式 解説 学校よりわかりやすいサイト




倍数と約数再び 正しい理解のために 身勝手な主張



問題文は 24の倍数で正の約数が15個であるような自然数を求めよ という Yahoo 知恵袋




よりくわ数学a 約数と倍数 教科書より詳しい高校数学




倍数と約数




心に強く訴える 公倍数 公約 数




高校数学 数a 勉強動画 約数と倍数 の問題 19ch




小学5年生の算数 整数の性質 偶数 奇数 約数 倍数 素数 練習問題プリント ちびむすドリル 小学生




小5 算数 小5 約数 公約数 最大公約数 Youtube




高校数学 整数の性質をわかりやすく解説 約数の個数やユークリッドの互除法も 高校生向け受験応援メディア 受験のミカタ




倍数と約数再び 正しい理解のために 身勝手な主張




倍数 約数 算数用語集




高校生 約数と倍数のノート一覧 Clear




整数の性質 最大公約数と最小公倍数について 日々是鍛錬 ひびこれたんれん




4講 整数のわり算と商 余り 1節 約数と倍数 問題集 3章 整数の性質




競プロ 素因数分解と約数と倍数 なかけんの数学ノート



約数 公約数 最大公約数 約分 分数のたし算ひき算の授業 教材 算数5年生の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材




数aに関する記事一覧 中学生 小学生 高校生のテストや受験対策に おすすめ無料学習問題集 教材サイト




約数 倍数とは その求め方 数a Youtube



高校生必見 高校生のための 無料映像授業 高校生ライフ




高校数学 数a 勉強動画 約数と倍数 の問題 19ch




高1 数学a 2章 1節 約数と倍数 3節 整数の性質の活用 高校生 数学のノート Clear



整数の性質 最大公約数 最小公倍数の求め方と性質をイチから解説 数スタ




倍数と約数について 基本的な事項にもどって 身勝手な主張




1講 約数と倍数 1節 約数と倍数 問題集 3章 整数の性質



1




中学受験算数 約数 ゼロから始める中学受験算数6 たったこれだけ 約数と倍数の最強攻略法 Youtube




最大公約数と最小公倍数の積の性質の2通りの証明 高校数学の美しい物語




2講 最大公約数 最小公倍数 1節 約数と倍数 問題集 3章 整数の性質




倍数と約数



約数と倍数高校数学 今日は日曜日で 10日後は水曜である 100日後およ Yahoo 知恵袋




整数の性質 約数の利用 Youtube




整数の性質 最大公約数 最小公倍数の求め方と性質をイチから解説 数スタ




新企画 合判模試の準備をしよう 基礎編 倍数 約数 受験情報ブログ 首都圏模試センター




小学5年生の算数 動画 倍数 約数の文章題の問題 19ch




最大公約数の求め方 素因数分解を使った解き方のコツとは 高校生向け受験応援メディア 受験のミカタ




倍数と約数とは 大人の学び直し算数 計算のやり方解説 無料




倍数と約数




最大公約数の求め方 素因数分解を使った解き方のコツとは 高校生向け受験応援メディア 受験のミカタ




中学数学より4 教科書に登場しない最小公倍数 最大公約数 身勝手な主張




約数と倍数 の勉強法のわからないを5分で解決 映像授業のtry It トライイット



1




高校生 約数と倍数のノート一覧 Clear



高校数学約数と倍数の問題ですり こちらの問いの139番が分 Yahoo 知恵袋



約数 公約数 最大公約数 約分 分数のたし算ひき算の授業 教材 算数5年生の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材




高校数学b 等差数列を利用する倍数の和 受験の月




高校数学a 倍数の証明問題 映像授業のtry It トライイット




高校数学 数a 勉強動画 約数と倍数 の問題 19ch




高校数学a 約数と倍数 整数問題の極意 受験の月



高校数学約数と倍数の問題ですり こちらの問いの139番が分 Yahoo 知恵袋




高校生 約数と倍数のノート一覧 Clear



整数の性質 最大公約数と最小公倍数について 日々是鍛錬 ひびこれたんれん



整数の性質 最大公約数と最小公倍数について 日々是鍛錬 ひびこれたんれん



高校1年生数学aの範囲です 約数と倍数です なんでこうなるんですか Yahoo 知恵袋




約数と倍数 の勉強法のわからないを5分で解決 映像授業のtry It トライイット




倍数と約数とは 大人の学び直し算数 計算のやり方解説 無料
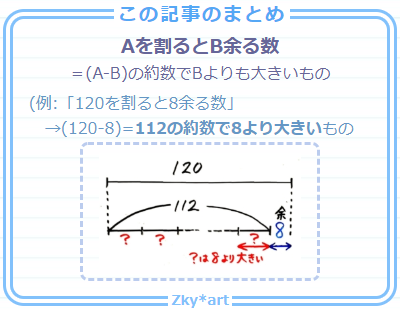



中学受験 約数と余りの問題 を 割ると余りが出る数 の求め方 そうちゃ式 受験算数 新1号館 数論 特殊算




整数問題の解法 高校数学ブログ




数a 28の倍数で正の約数の個数が15こである自然数nを全て求めよ とい 数学 教えて Goo




最大公約数と最小公倍数の求め方とは ヒント 素因数分解 遊ぶ数学




โน ตของ 数学a 整数の性質 ช น Senior High数学 Clear
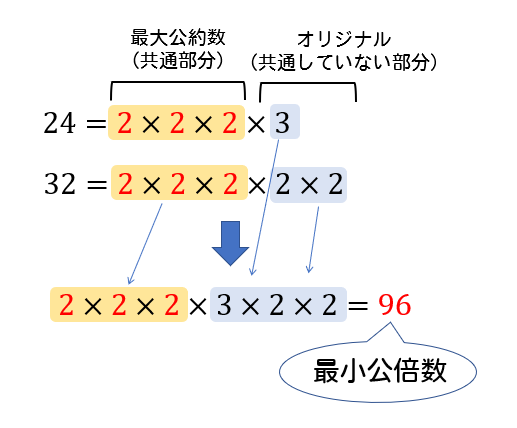



整数の性質 最大公約数 最小公倍数の求め方と性質をイチから解説 数スタ



3




高校数学a 倍数の証明問題 練習編 映像授業のtry It トライイット




高校数学a 最大公約数の求め方 映像授業のtry It トライイット




Ookubotact 大久保 中二病中年 超算数 高校数学の倍数の記述に関して 数研版の記述について 教科書ガイドを3種類見てみた




1講 約数と倍数 1節 約数と倍数 問題集 3章 整数の性質




よりくわ数学a 約数と倍数 教科書より詳しい高校数学




約数と倍数 の勉強法のわからないを5分で解決 映像授業のtry It トライイット




最大公約数の求め方 素因数分解を使った解き方のコツとは 高校生向け受験応援メディア 受験のミカタ




倍数と約数とは 大人の学び直し算数 計算のやり方解説 無料




249の問題が分かりません nをすべて求めよ という問題です Clear




1講 約数と倍数 1節 約数と倍数 問題集 3章 整数の性質




教科書レベルの問題一覧と解答 数学a 整数の性質 教科書より詳しい高校数学




中学受験 算数確認チェック13 数の性質 約数 倍数 グランパは元塾長



Q Tbn And9gcrz4tiiujvjvtvxv2ozmm Mvsq9zohcodw0yyuasqa Asxohv5b Usqp Cau
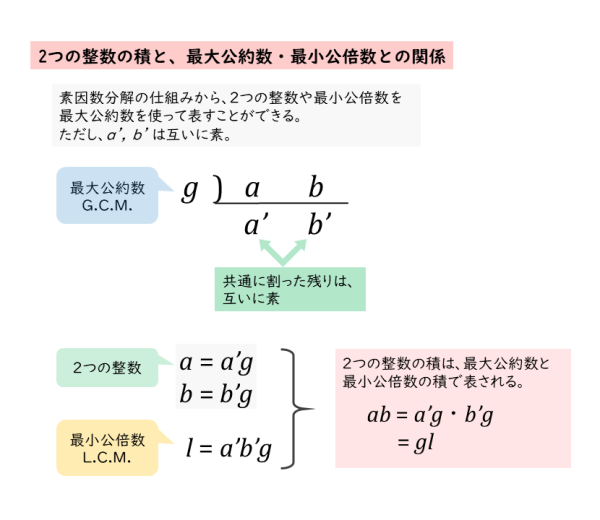



整数の性質 最大公約数と最小公倍数について 日々是鍛錬 ひびこれたんれん




高校数学 数a 65 約数と倍数 Youtube




高校数学a 3の倍数 9の倍数の見分け方 映像授業のtry It トライイット




複数の整数の最大公約数と最小公倍数について 高校数学マスター




高校数学a 約数の求め方 映像授業のtry It トライイット




約数の個数と約数の総和の求め方とは 公式は素因数分解で導きます 遊ぶ数学




倍数と約数 倍数の個数 重要 算数の教え方教えますmother S Math Happy Study Support




小学5年生の算数 整数の性質 偶数 奇数 約数 倍数 素数 練習問題プリント ちびむすドリル 小学生




倍数の個数の求め方 数学 苦手解決q A 進研ゼミ高校講座




ラブリー 倍数 の 求め 方 壁紙 配布




数aの整数 約数と倍数の分野です 赤チャートです 教えてくださいっm M Clear




高校数学 整数の性質をわかりやすく解説 約数の個数やユークリッドの互除法も 高校生向け受験応援メディア 受験のミカタ




3講 最大公約数 最小公倍数の性質 1節 約数と倍数 問題集 3章 整数の性質




約数と倍数 の勉強法のわからないを5分で解決 映像授業のtry It トライイット



0 件のコメント:
コメントを投稿